RHme3オンライン予選の第2問のWriteUpです。
第2問
問題名:Tracing the Traces
問題文:These traces (.trs and .mat format) were captured from a hardware device performing a certain cryptographic calculation. The trace files contain input/output data as well as the corresponding power measurements for (part of) the cryptographic operation. Can you get the key?
問題ファイル:overview.png, traces.mat, traces.trs
問題ファイルの解析
ハードウェア実装された暗号アルゴリズムのトレースデータ(の一部)を解析し、鍵を抽出する問題です。 overview.pngは、暗号化(復号)処理全体の電力波形のようです。
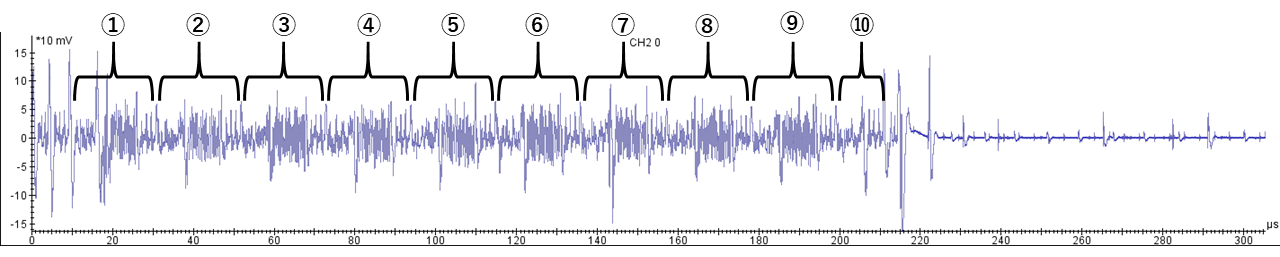
①から⑨には波形が密な部分があります。 ⑩には密な部分はありませんが、①から⑨の密な部分の前後の波形と似た波形をしています。 このことから、10回同じ処理を繰り返す、但し10回目は少し異なる、ということが分かります。 第1問のWriteUpを読んで頂いた方は、すぐにお分かりだと思います。 暗号アルゴリズムは「AES-128」です(∵AES-128は全10ラウンドあり、第10ラウンドではMixColumnsを行わない)。
次に、traces.matを見ます。
$ head -10 traces.mat
# Created by Octave 4.0.3, Fri Aug 04 14:04:39 2017 CEST <andres@kali-andres>
# name: inout
# type: int8 matrix
# ndims: 2
300 32
42
-31
33
93
-68
GNU Octaveで作成されているので、Octaveで読み込みます。
> load("traces.mat")
> whos
Variables in the current scope:
Attr Name Size Bytes Class
==== ==== ==== ===== =====
inout 300x32 9600 int8
samples 300x6095 7314000 single
Total is 1838100 elements using 7323600 bytes
平文と暗号文のペア(inout)と対応するトレースデータ(samples)が300個ずつあるようです。 続いて、トレースデータ(samples)が暗号化(復号)処理のどの部分をトレースしたものであるかを特定するために、トレースデータの1つをプロットします。
> plot(samples(1,:))
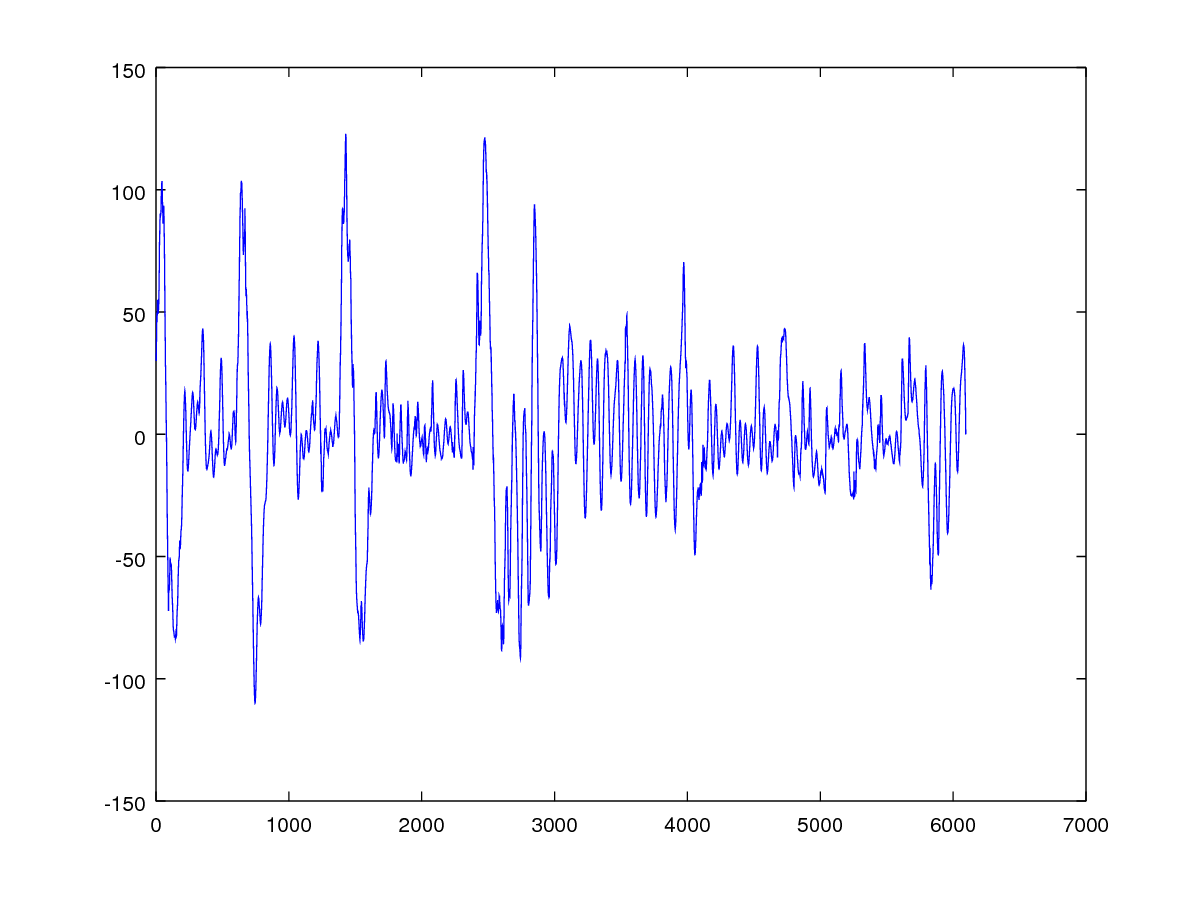
overview.pngと比較すると、暗号化(復号)処理の最初の部分をトレースしたものであると分かります。 従って、暗号化(復号)処理の第1ラウンドに対して、攻撃を行えば良いようです。
traces.trsはファイル形式が分からず読み込めませんでした。ファイル形式が異なるだけで、中身のデータはtraces.matと同じだと思います。
鍵の抽出
鍵の抽出のために、差分電力解析(DPA:Differential Power Analysis)を行います。 DPAはPaul Kocherらによる論文「Differential Power Analysis」[1]で発表されました。 当該論文ではDESに対するDPAの適用が説明されていますが、AESに対しても手法は同じです。 DPAでは、最初に選択ビットを仮定します。 選択ビットとは、そのビットの値が1であるか0であるかによって、トレースデータをグループ分けすることで、各々のグループの平均電力間の差が大きく、ピークが発生すると予想されるビットのことです。 ラウンド鍵(当該問題では第1ラウンド)を総当たりしながら、選択ビットによってトレースデータをグループ分けします。 もし、ラウンド鍵が正しければ、選択ビットの値が1であるグループと0であるグループに正しく分けられるため、選択ビット処理時の電力に差が生じ、ピークが発生します。 ピークが最大となるときのラウンド鍵が、正しいラウンド鍵です。 DPAは式(1)([1], p.5)で表されます。
$$\Delta D[j] = \frac{\sum_{i=1}^{m} D(C_i,b,K_s) T_i[j]}{\sum_{i=1}^{m} D(C_i,b,K_s)} - \frac{\sum_{i=1}^{m} (1-D(C_i,b,K_s)) T_i[j]}{\sum_{i=1}^{m} (1-D(C_i,b,K_s))} \qquad (1)$$
$\Delta D[j]$がトレースポイント$j$(当該問題では、$0 \leq j \lt 6095$)における、各々のグループの平均電力間の差です。 $T_i[j]$は$i$個目のトレースデータのトレースポイント$j$における消費電力です。 $m$はトレースデータの個数で、当該問題では$m=300$です。 $D(C_i,b,K_s)$は選択関数と呼ばれ、暗号文$C_i$と予測鍵$K_s$から計算される選択ビット$b$の値(i.e. 0または1)を表します。 暗号化処理の第1ラウンド、または復号処理の第10ラウンドに対してDPAを行う場合、暗号文$C_i$の代わりに平文$P_i$を用います。 従って、暗号化処理の第1ラウンドのSubBytesに対してDPAを行う場合、平文$P_i$と予測鍵$K_s$の$x(0 \leq x \lt 16)$byte目をそれぞれ$P_{i,x}$、$K_{s,x}$、関数$S_b$をSubBytes出力の$b(0 \leq b \lt 8)$bit目とすると、選択関数$D$は式(2)で表されます。
$$D(P_{i,x},b,K_{s,x}) = S_b(P_{i,x} \oplus K_{s,x}) \qquad (2)$$
実際にDPAを行う場合、トレースポイント$j$を1ずつ変えながら攻撃をするのは非効率なので、一定の範囲内での消費電力差の最大値$\max \{\Delta D[j] \mid \alpha \leq j \leq \beta\}$($\alpha$, $\beta$は0以上トレースポイント数以下)を計算します。 「データブロックの0bit目が1のとき、1bit目も必ず1である。」のような選択ビット間での相関が無ければ、この方法で問題ありません。
式(1)、(2)を用いて、DPAを試みました。
しかし、ピークが発生しませんでした。
複数の予測鍵$K_{s,x}$において、消費電力差の最大値$\max \{\Delta D[j] \mid \alpha \leq j \leq \beta\}$が同程度になっています。
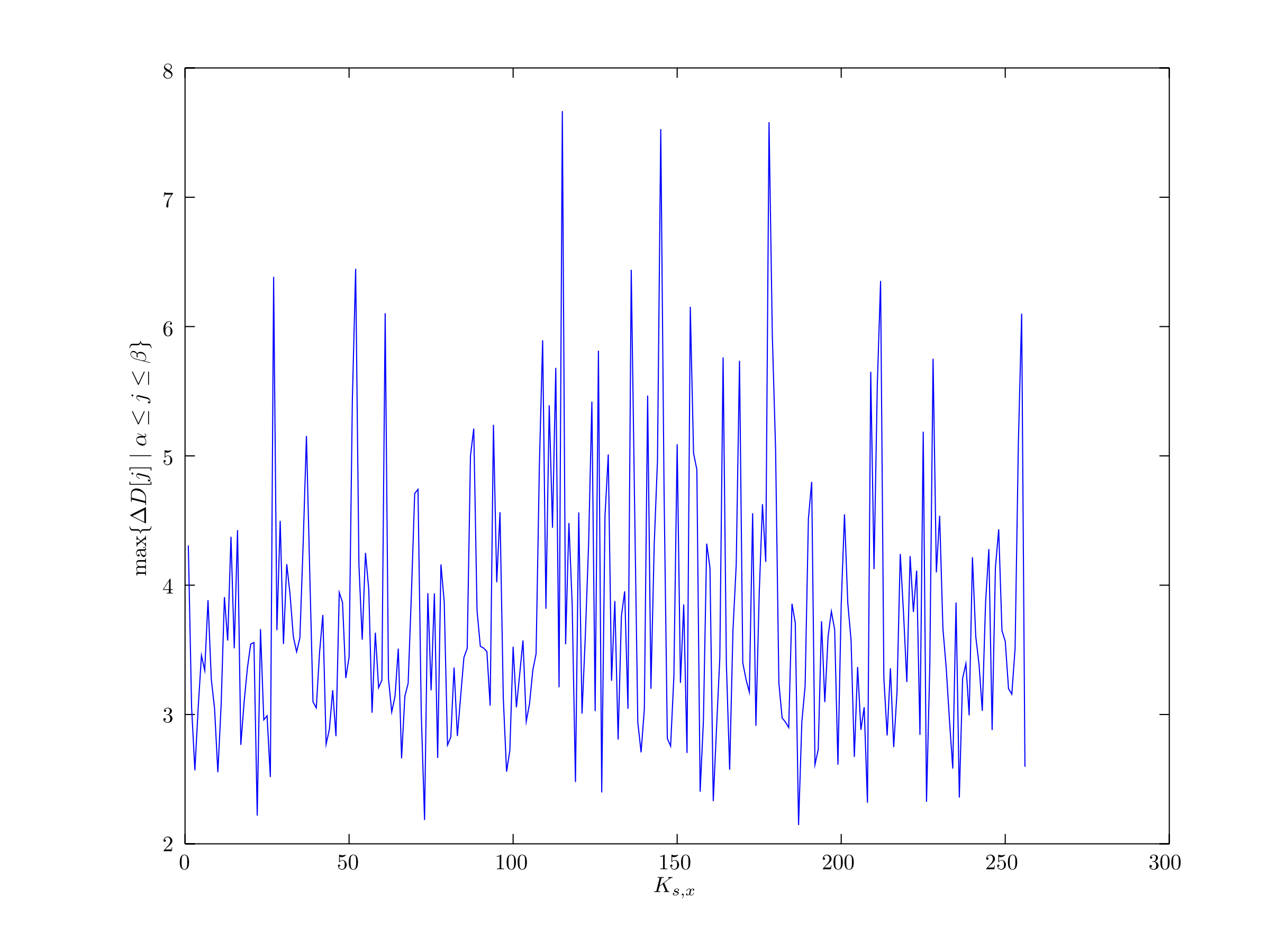
($x = 0,\ b = 0,\ \alpha = 1600,\ \beta = 2300$)
選択ビット$b$やトレースポイント$j$を変更し、何度も攻撃を行いましたが、同様の結果でした。
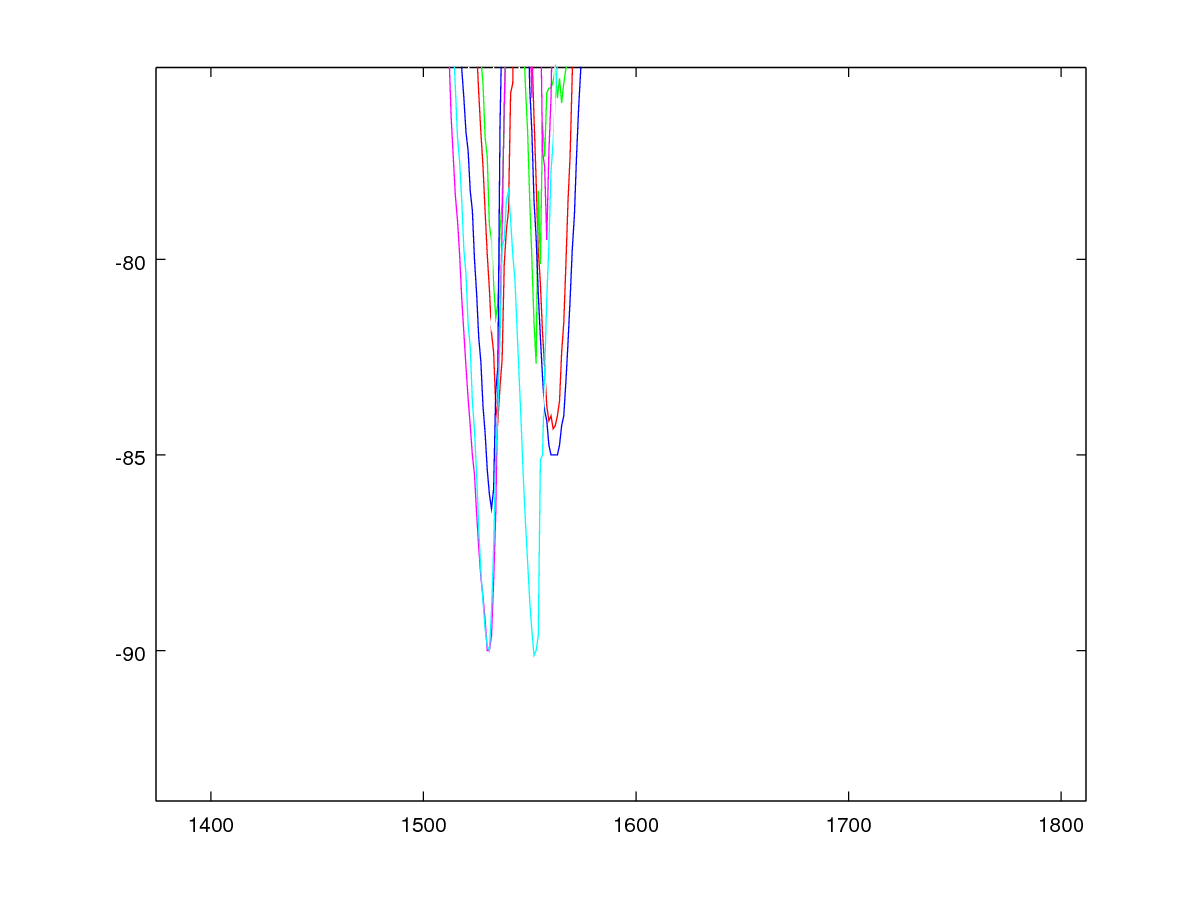
ここで、トレースデータのいくつかを同じグラフ上にプロットしてみると、波形がズレている(i.e. ジッタ―が存在する)ことに気が付きました。
> hold on
> plot(samples(1,:),"r");
> plot(samples(2,:),"g");
> plot(samples(3,:),"b");
> plot(samples(4,:),"m");
> plot(samples(5,:),"c");
> plot(samples(6,:),"w");
ジッターを補正するプログラムを作成するのは面倒なので、願いを込めながらGoogleやGitHubで検索します。 GitHubにて「side channel」で検索し、スター降順でソートしたところ、トップに「ChipWhisperer」[2]というツールがヒットしました。 当該ツールは、平文・暗号文・トレースデータなどを「.npy」ファイル(numpyのndarrayデータを保存するためのバイナリ形式のファイル)で読み込ませることで、電力解析攻撃を行うようです。 Wikiを眺めていると攻撃前処理として、ジッター補正が可能だと分かりました[3]。 神は居るものです。 攻撃アルゴリズムにはDPAではなくCPA(Correlation Power Analysis)を用いるようです。 CPAはEric Brierらによる論文「Correlation Power Analysis with a Leakage Model」[4]で発表されました。 CPAは式(3)([4], p.5)で表されます。
$$ \begin{eqnarray} \left\{ \begin{array}{l} \hat{\rho}_{WH}(R) = \frac{N \sum W_i H_{i,R} - \sum W_i \sum H_{i,R}} {\sqrt{N \sum W^2_i - (\sum W_i)^2} \sqrt{N \sum H^2_{i,R} - (\sum H_{i,R})^2}}\\ H_{i,R} = H(M_i \oplus R)\\ \end{array} \right. \end{eqnarray} \qquad (3) $$
$\sum = \sum^{N}_{i=1}$で、$N$はトレースデータの個数です。 消費電力$W_i$と対応するメッセージ$M_i$(平文$P_i$または暗号文$C_i$)が与えられたとき、メッセージ$M_i$と基準状態$R$のハミング距離$H_{i,R} = H(M_i \oplus R)$を計算し、消費電力$W_i$との相関(ピアソンの積率相関係数の推定値$\hat{\rho}_{WH}(R)$)が最大になるような予測鍵$K_s$を探索します。 ハミング距離$H_{i,R}$が大きければ反転するビット数も多いので、消費電力も大きいであろうということです。 基準状態$R$は、例えば、暗号化処理の第1ラウンドのSubBytesに対してCPAを行う場合、$R = S_b(M_{i,x} \oplus K_{s,x})$になります。 ただし、メッセージ$M_i$の$x$byte目の$b$bit目を$M_{i,x,b}$として、ハミング距離$H_{i,R} = H(M_{i,x,b} \oplus R)$であり、また、DPAと異なり選択ビット$b$は複数ビットです(e.g. 0bit目から7bit目まで)。 また、ピアソンの積率相関係数(の推定値)は式(4)の形式で見ることが多いと思います。
$$\hat{\rho}_{WH}(R) = \frac{\sum (W_i - \bar{W})(H_{i,R} - \bar{H}_R)} {\sqrt{\sum (W_i - \bar{W})^2} \sqrt{\sum (H_{i,R} - \bar{H}_R)^2}} \qquad (4)$$
証明は省略しますが、式(3)は式(4)の$\bar{W}$と$\bar{H}_R$をそれぞれ$\frac{1}{N} \sum W_i$、$\frac{1}{N} \sum H_{i,R}$で置き換えて式変形をしただけなので等価です。
当該ツールを用いて鍵の抽出を試みます。
WikiのFile Formats解説ページ[5]を参考に、設定ファイル(.cfg)とデータファイル(.npy)を作成します。
暗号化処理の第1ラウンドのSubBytesに対して攻撃を行うため、SubBytesを行っていると思われる部分にジッター補正機能を適用します。
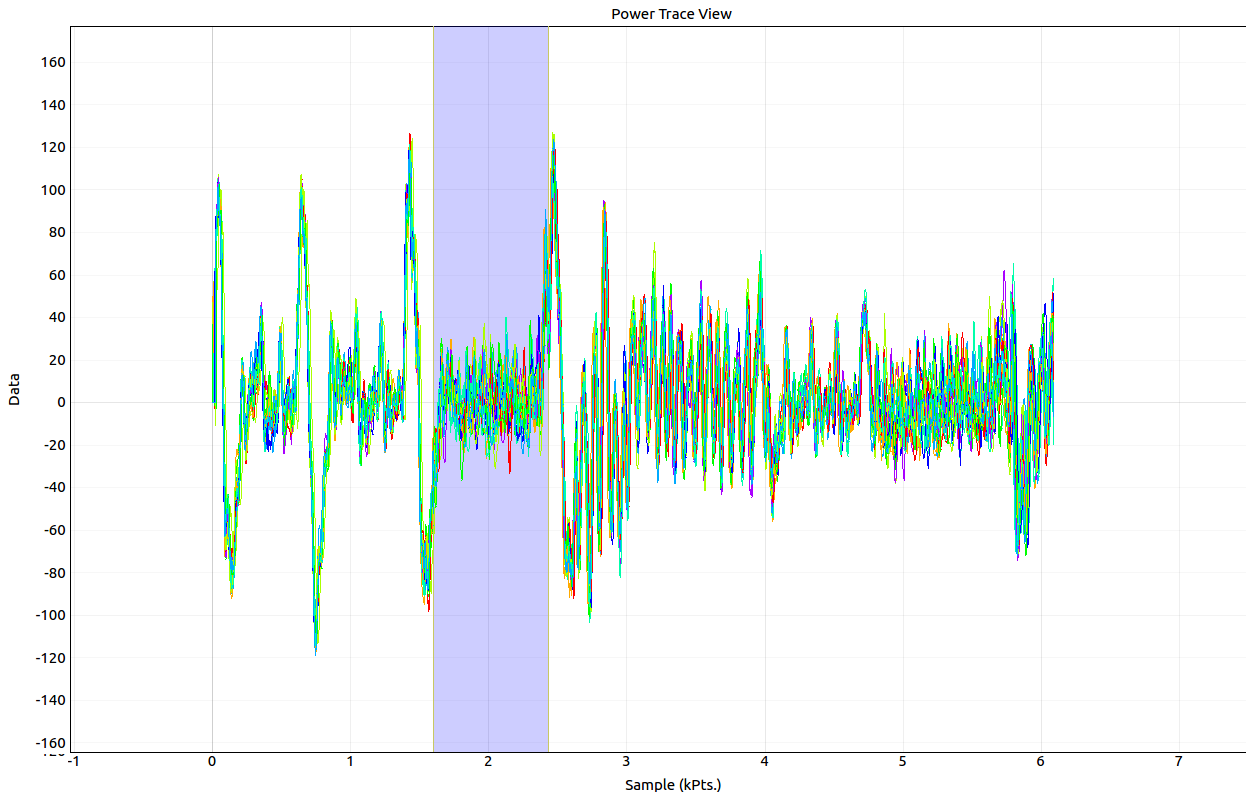
攻撃を実行すると、数分で終了し、ラウンド鍵を1byteごとにランク付けした結果が表示されました。
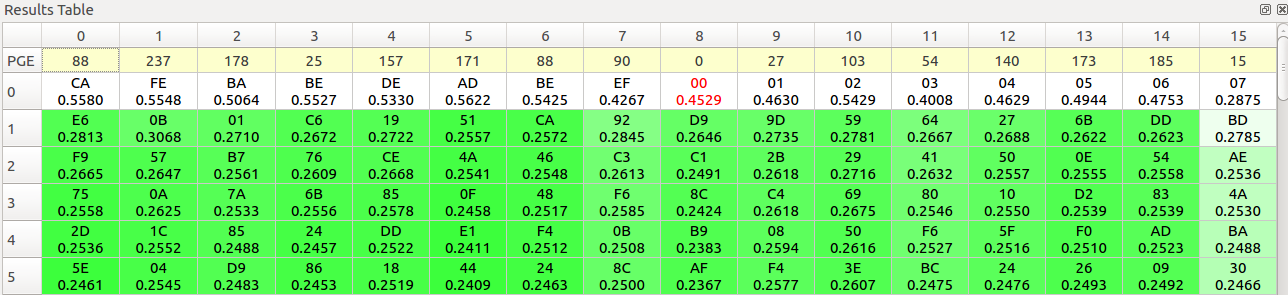
0番目にランク付けされた値が最も正しいと思われるラウンド鍵の値です。
CAFEBABEDEADBEEF0001020304050607
この文字列がFlagでした。
今回の問題は、神ツール「ChipWhisperer」(または同等のもの)を知っていれば30分で解ける問題でした。 悲しいです。 次回は、Exploitに関する問題です。
参考・引用文献
- Paul Kocher, Joshua Jaffe, and Benjamin Jun. Differential Power Analysis, pp. 388{397. Springer Berlin Heidelberg, Berlin, Heidelberg, 1999.
- ChipWhisperer® by NewAE Technology Inc.. GitHub - newaetech/chipwhisperer: ChipWhisperer - the complete open-source toolchain for side-channel power analysis and glitching attacks, <https://github.com/newaetech/chipwhisperer>2017年9月14日アクセス
- ChipWhisperer® by NewAE Technology Inc.. Sum of Absolute Difference (SAD) Pre-Processing - ChipWhisperer Wiki, <https://wiki.newae.com/Sum_of_Absolute_Difference_(SAD)_Pre-Processing>2017年9月14日アクセス
- Eric Brier, Christophe Clavier, and Francis Olivier. Correlation Power Analysis with a Leakage Model, pp. 16-29. Springer Berlin Heidelberg, Berlin, Heidelberg, 2004.
- ChipWhisperer® by NewAE Technology Inc.. File Formats - ChipWhisperer Wiki, <https://wiki.newae.com/File_Formats>2017年9月14日アクセス





